By Jocelyn Hitchcock, Contributing Writer, Classical Wisdom
We all know the varsity team: Einstein, Newton, Pythagoras, Descartes. These names are drilled into our heads all through grade school math and history classes, and possibly accompanied by an under-the-breath curse from a disgruntled calculus or physics student. However, another mathematician should receive our attention: Euclid of Alexandria.
It is difficult to underscore enough the importance and significance of Euclid and his impact on mathematics for the subsequent 2000 years. Nonetheless, we will try.

Euclid of Alexandria
Euclid’s Early Life
The documentation of
Euclid’s life is scant, at best. While we have a great deal of his work in extant, facts about Euclid as a person come down to us mainly through little snippets by Proclus and Apollonius (among others).
Proclus, a Greek philosopher living in the 5th century CE, writes retrospectively and so his information must be taken with a grain of salt. He writes that Euclid taught in
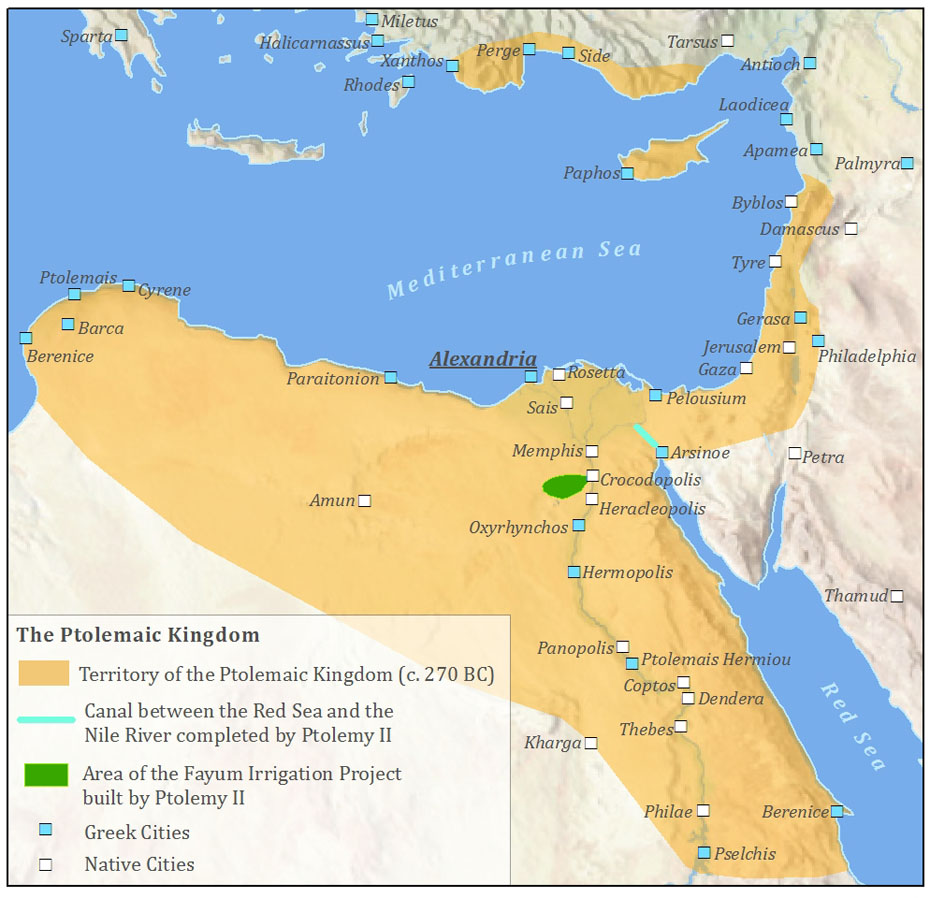
Alexandria, Egypt during the time of
Ptolemy I Soter (4th-3rd century BCE). This places him as younger than Plato, but slightly older than Archimedes. Euclid was likely born around 300 BCE and resided in Alexandria, Egypt for most, if not all, of his life. Some historians think that he might have studied for a bit at Plato’s Academy in Athens, but this is conjecture based on his style of teaching. Past this, nothing is known of Euclid.

Map Showing Alexandria, Egypt, birthplace of Euclid
Euclid’s Career
Often called the “Father of Geometry,” Euclid was a teacher of mathematics, cultivating a school of pupils not unlike the style of the Academy. Proclus writes that Ptolemy once asked Euclid if there was a “shortened way to study geometry than the Elements, to which Euclid replied that there was no royal road to geometry.” This would suggest that not only was Euclid noteworthy among mathematicians and scientists in Alexandria, but was prominent enough to have an audience with the ruler of Egypt. As with details of his early life, we don’t know specifics regarding his career, save for his extant works and the fact that he was a prominent teacher in Alexandria.
Euclid’s Works and Achievements
Euclid likely wouldn’t have reached his level of renown if his works didn’t survive to such an incredible extent. His main work, The Elements, is a proto-textbook of 13 sections pulling together definitions, theories, and constructions of mathematics at the time. He covers geometry, number theory, and incommensurate lines- all subjects that have proved to be invaluable over the development of mathematics.

The cover of Euclid’s Elements
The Elements consisted of five general axioms and five geometrical postulates. Euclid provided the basic model for mathematical argument that follows logical deductions from initial assumptions. For those of us (including myself) who are not so mathematically inclined to understand the nitty-gritty details of Euclid’s Elements, Sir Thomas Heath sums them up in his 1908 publication The Elements of Euclid:
The 5 Axioms of Euclid:
1. Things which are equal to the same thing are also equal to one another
2. If equals are added to equals, the whole (sums) are equal
3. If equals are subtracted from equals, the remainders (differences) are equal
4. Things that coincide with one another are equal to one another
5. The whole is greater than the part
The 5 Geometric Postulates:
1. It is possible to draw a straight line from any point to any point
2. It is possible to extend a finite straight line continuously in a straight line
3. It is possible to create a circle with any center and distance
4. All right angles are equal to one another
5. If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the straight lines, if produced indefinitely, will meet on that side on which the angles are less than two right angles.
Other important contributions from Euclid is his proof of
Pythagoras‘ Theorem, providing us with formulas that calculate the volumes of solids like cones, pyramids, and cylinders, as well as identifying the first four ‘
perfect numbers,’ among a dozen or so other theories and proofs.

The most famous proposition from The Elements, Proposition 1.47. Also known as the Pythagorean Theorem.
In addition to the Elements, five other works of Euclid have come down to us and have been able to be interpreted: Data, dealing with the nature and implications of “given” information in geometry; On Divisions of Figures, dealing with the division of geometrical figures into two or more equal parts or into parts in given ratios; Catoptrics, dealing with the theory of mirrors and the images formed in plane and spherical concave mirrors; Phaenomena, a treatise on spherical astronomy; and Optics the earliest surviving Greek treatise on perspective.
Euclid’s Death and Legacy

Euclid of Alexandria
We can assume that Euclid died in the mid-3rd century BCE in Alexandria, but that is all we know. However, he left behind a legacy that has survived almost two and a half millennia. His work on geometry and theory is still in use today, governing even advanced models of dimension mathematics. He is considered one of the greatest mathematicians to have ever lived, and a European Space Agency’s spacecraft was even named in his honor, the Euclid Spacecraft.













One comment
Proclus Diadochus, in his Commentary on Euclid’s Elements, relates the history of geometry up to the time of Euclid. The following extract is taken from his commentary on Book I:-
We must next speak of the origin of geometry in the present world cycle. For, as the remarkable Aristotle tells us, the same ideas have repeatedly come to men at various periods of the universe. It is not, he goes on to say, in our time or in the time of those known to us that the sciences have first arisen, but they have appeared and again disappeared, and will continue to appear and to disappear, in various cycles, of which the number both past and future is countless. But since we must speak of the origin of the arts and sciences with reference to the present world cycle, it was, we say, among the Egyptians that geometry is generally held to have been discovered. It owed its discovery to the practice of land measurement. For the Egyptians had to perform such measurements because the overflow of the Nile would cause the boundary of each person’s land to disappear. Furthermore, it should occasion no surprise that the discovery both of this science and of the other sciences proceeded from utility, since everything that is in the process of becoming advances from the imperfect to the perfect. The progress, then, from sense perception to reason and from reason to understanding is a natural one. And so, just as the accurate knowledge of numbers originated with the Phoenicians through their commerce and their business transactions, so geometry was discovered by the Egyptians for the reason we have indicated.
It was Thales, who, after a visit to Egypt, first brought this study to Greece. Not only did he make numerous discoveries himself, but laid the foundations for many other discoveries on the part of his successors, attacking some problems with greater generality and others more empirically. After him Mamercus, the brother of the poet Stesichorus, is said to have embraced the study of geometry, and in fact Hippias of Elis writes that he achieved fame in that study.
After these Pythagoras changed the study of geometry, giving it the form of a liberal discipline, seeking its first principles in ultimate ideas, and investigating its theorems abstractly and in a purely intellectual way. It was he who discovered the subject of proportions and the construction of the cosmic figures. After him Anaxagoras of Clazomenae devoted himself to many of the problems of geometry, as did Oenopides of Chios, who was a little younger than Anaxagoras. Plato in The Rivals mentions them both as having achieved repute in mathematics. After them Hippocrates of Chios the discoverer of the quadrature of the lune, and Theodorus of Cyrene gained fame in geometry. For Hippocrates is the first man on record who also composed Elements.
Plato, who lived after Hippocrates and Theodorus, stimulated to a very high degree the study of mathematics and of geometry in particular because of his zealous interest in these subjects. For he filled his works with mathematical discussions, as is well known, and everywhere sought to awaken admiration for mathematics in students of philosophy.
At this time lived also Leodamas of Thasos, Archytas of Tarentum, and Theaetetus of Athens, all of whom increased the number of theorems and made progress towards a more scientific ordering thereof. Neoclides and his pupil, Leon, who were younger than Leodamas, made many additions to the work of their predecessors. As a result the Elements composed by Leon are more carefully worked out both in the number and in the usefulness of the propositions proved. Leon also first discussed the diorismi (distinctions), that is the determination of the conditions under which the problem posed is capable of solution, and the conditions under which it is not.
A little younger than Leon was Eudoxus of Cnidus, an associate of Plato’s school, who first increased the number of the general theorems, as they are called, and added three new proportions to the three then known. Using the method of analysis he greatly extended the theory of the section, a subject which had originated with Plato. Amyclas of Heraclea, a friend of Plato, Menaechmus, a pupil of Eudoxus who had also been associated with Plato, and Dinostratus, a brother of Menaechmus, brought the whole of geometry to an even higher degree of perfection. Theudius of Magnesia achieved a reputation for excellence both in mathematics and in the other parts of philosophy, for his Elements were excellently arranged and many of the (theretofore) limited propositions were put in more general form. Furthermore, Athenaeus of Cyzicus, a contemporary, distinguished himself in mathematics generally and in geometry in particular. These men spent their time together in the Academy and collaborated in their investigations. Hermotimus of Colophon extended the work that had been done by Eudoxus and Theaetetus, made many discoveries in the Elements, and put together some material on the subject of Loci. Philippus of Mende who, as a pupil of Plato, was inspired by him to the study of mathematics, conducted investigations along lines suggested by Plato, and in particular set before himself researches which he thought would contribute to the philosophy of Plato. Now those who have written histories trace the development of the science of geometry down to Philippus.
Euclid, who was not much younger than Hermotimus and Philippus, composed Elements, putting in order many of the theorems of Eudoxus, perfecting many that had been worked on by Theaetetus, and furnishing with rigorous proofs propositions that had been demonstrated less rigorously by his predecessors. Euclid lived in the time of the first Ptolemy, for Archimedes, whose life overlapped the reign of this Ptolemy too, mentions Euclid. Furthermore, there is a story that Ptolemy once asked Euclid whether there was any shorter way to a knowledge of geometry than by the study of the Elements. Whereupon Euclid answered that there was no royal road to geometry. He is, then, younger than Plato’s pupils and older than Eratosthenes and Archimedes, who, as Eratosthenes somewhere remarks, were contemporaries.
By choice Euclid was a follower of Plato and connected with this school of philosophy. In fact he set up as the goal of the Elements as a whole the construction of the so-called Platonic figures.
There are, in addition, many other mathematical works by Euclid, written with remarkable accuracy and scientific insight, such as the Optics, the Catoptrics, works on the Elements of Music, and the book On Divisions. But he is most to be admired for his Elements of Geometry because of the choice and arrangement of the theorems and problems made with regard to the elements. For he did not include all that he might have included, but only those theorems and problems which could fulfil the functions of elements …. If you seek to add or subtract anything, are you not unwittingly cast adrift from science and carried away toward falsehood and ignorance?
Now there are many things that seem to be grounded in truth and to follow from scientific principles but actually are at variance with these principles and deceive the more superficial. It was for this reason that Euclid set forth methods for intelligent discrimination in such matters, too. With these methods not only shall we be able to train beginners in this study to detect fallacies, but we shall be able to escape deception ourselves. The work in which he gives us this preparation he entitled Pseudaria. In it he recounts in order various types of fallacies, training us to understand each type by all sorts of theorems, setting the true alongside the false, and linking the refutation of the fallacy with empirical examples. This book, therefore, is for the purification and training of the understanding, while the Elements contain the complete and irrefutable guide to the scientific study of the subject of geometry.
http://www-history.mcs.st-andrews.ac.uk/Extras/Proclus_history_geometry.html
Trackbacks
Our apologies, you must be logged in to post a comment.