By Jacob Bell, Associate Editor, Classical Wisdom
Zeno of Elea constructed several arguments that result in absurdity. They are paradoxical, contradicting, and just plain-strange. Oh, and did I mention that they are logically consistent, too?
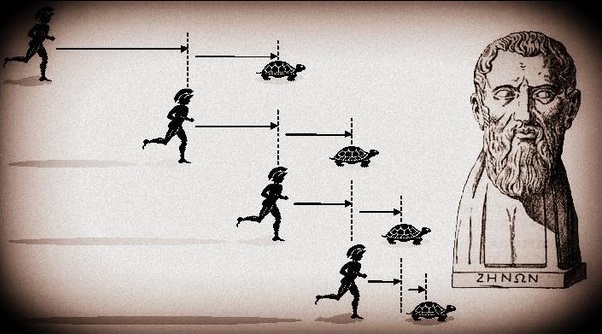
One such paradox, perhaps the most well-known, is called the Achilles Paradox. Achilles was thought to be the fastest runner in Ancient Greece, and as such he should have no problem running down a tortoise, right? Zeno thinks not, and has a really good argument for why not.

Zeno of Elea
Alright, imagine Achilles and the tortoise, and let’s refer to the tortoise as Tom, because, well, a tortoise that races Achilles should probably have a name. Okay, so it is Achilles and Tom the tortoise at the starting line for this historical race. Since Achilles is the fastest man in Greece, he decides that it would only be fair to give Tom a head start.
Tom starts his crawl while Achilles poses and flexes for the crowd! What a showman! After a few moments Achilles takes off after Tom. According to Zeno, Achilles will never catch up to Tom because there is an infinite number of points between Achilles and Tom. Therefore Achilles can never reach Tom, because he cannot traverse an infinite number of points!
Before Achilles reaches Tom, he must first get half way to Tom. Before he can get half way to Tom, he must get a quarter of the way to Tom, before he can get a quarter of the way, he must go an eighth of the way… and so on ad infinitum. According to Zeno’s logically consistent argument, Achilles will never reach Tom. Sorry to all you runners out there.

The Achilles Paradox
But wait just a minute… We all know from experience that a faster runner can, and will, catch a slower runner. So just what in the world-of-Hades is going on here? As I mentioned earlier, Zeno remains logically consistent within his argument. So it is not a problem of logic. Let’s look at his assumptions.
Zeno is constructing his argument on the foundational assumption that the world is infinitely divisible. If we change this assumption, the problem magically goes away. Hey, Zeno… the world isn’t infinitely divisible, therefore there is only a finite number of points that Achilles must travel in order to catch Tom. (Sorry, Tom.)
It may be worthwhile to point out that some mathematicians overcome this paradox with calculus and something called the convergence of finite-infinite series. Others argue against this method. But I digress. Let us explore the world of abstraction and the world as experienced.
When we first encounter the Achilles Paradox, we become suspicious. After all, the paradox is fundamentally at odds with the way we experience the world. The logic of the argument works, but it doesn’t coincide with the way the world really is. Arguments which are logically sound and logically true, don’t always accurately represent nature, reality, or the world. The same can be said for mathematics.

Artistic Depiction of a Singularity
Let us look at the mathematical concept of a singularity as an example. Black holes are said to contain a singularity at their center, and the Big Bang supposedly started with one, too. Many physicists don’t actually believe that the Big Bang started with a singularity, and others question the whole idea that singularities exist in nature at all!
We all experience the mathematical singularity of draining our tub. When you drain the tub, the water spirals into the drain, moving faster and faster, and at a certain point, according to consistent mathematics, the water will be moving infinitely fast. This doesn’t actually happen the way that the math tells us it will. The world gets in the way, and the water doesn’t actually converge into a singularity like the math tells us it should. For some physicists and mathematicians, singularities are nothing but mathematical artifacts, as opposed to something that actually exists in nature.
Like Zeno’s argument, it is through the use of pure rationality that the existence of such a phenomenon is posited. Further, the argument rests on a set of assumptions that themselves have not been proven to be true.
In using the term rationality, I am referring to the epistemic view that regards the use of pure reason as the foundation of truth and the method for uncovering reality. Contrast this with the epistemic method of empiricism, which claims that truth is revealed to us through the senses.
Okay, so what does this all mean? Just like Zeno’s paradoxical arguments, there exists a great many of contemporary paradoxical arguments and contradicting concepts in logic and math. The assumptions used in creating an argument, concept, or mathematical equation are, from a historical point of view, usually false or only sort-of-true. If an assumption is false, the logic can maintain consistency and seem true within the logical context, but it might not be true of the world, and it might not be an accurate representation of nature.

It isn’t all for naught, however. Sometimes we are right (or sort of right)… and that’s something.












2 comments
Any one who takes Zeno’s paradox seriously is not worthy of being called a philosopher… It is a joke, worthy only of Aesop…
It’s major problem, like the black hole transition, is based on time, the great leveler of us all…
As Zeno’s runner is approaching his zero point, time is dilating… that is, in the jokester’s imagination… and your mind, the time segments involved are becoming halved by each step, therefore, in the paradoxical limitation constructed only in your mind, you are seeing the process in smaller and smaller increments… like in a calculus limitation series…
So, where does that leave us in terms of the paradoxical event horizon of a black hole?
Well, you see the same thing is happening, time is dilating, according to the mathematical “laws” of E equals MC squared philosophy… That is, as you are approaching this Zeno’s limit of a time-based “event horizon” the illusion of a limit and the impossibility of ever achieving your goal seems imminent…
These are the limitations of thinking in this Einsteinian-particle-based universe… in our mind… But! Quantum physics is beginning to show us the true light of reason, even as we are watching this Magical Mystery Tour of the Universe and letting our minds be fooled into thinking that the rabbit is still in the hat…
I don’t think I have met anyone that takes the Zeno Paradox seriously in the sense that they believe that it is a true reflection of reality. It is a fun thought experiment, and can be taken seriously within a particular context, for the sake of working through the logic of the problem. But its use is as an exercise of the mind, as opposed to something true of the world or a reflection of reality.
In regards to quantum physics showing us the true light of reason… it also has its problems. Which interpretation are you referring to? There are multiple systems of interpretation regarding quantum physics, and the conclusions change as the interpretations do. The “traditional” Copenhagen interpretation of quantum mechanics has been facing some serious challenges from the Pilot-Wave theory.
Things are never as simple as they seem, every theory has problems, and include assumptions which have not been proven to be true. Assumptions are necessary, of course, but as theories or interpretations change, assumptions change, and the conclusions change.
It will be interesting to see where quantum physics takes us, and where it runs into paradigmatic problems…
Thank you for the discussion!
Jacob
Trackbacks
Our apologies, you must be logged in to post a comment.